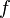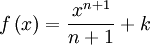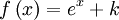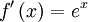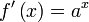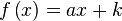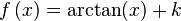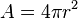jueves, 18 de abril de 2013

Métodos de integración

Se entiende por métodos de integración cualquiera de las diferentes técnicas elementales usadas para calcular una antiderivada o integral indefinida de una función.
Así, dada una función f(x), los métodos de integración son técnicas cuyo uso (usualmente combinado) permite encontrar una función F(x) tal que

$F(x) = \int f(x)\,\mathrm{d}x$ ,

lo cual, por el teorema fundamental del cálculo equivale a hallar una función F(x) tal que f(x) es su derivada:^{[notas 1]}

$\frac{d\,F(x)}{dx} = f(x)$ .

Concepto de integral definida

La integral definida es un concepto utilizado para determinar el valor de las áreas limitadas por curvas y rectas. Dado el intervalo [a, b] en el que, para cada uno de sus puntos x, se define una función f (x) que es mayor o igual que 0 en [a, b], se llama integral definida de la función entre los puntos a y b al área de la porción del plano que está limitada por la función, el eje horizontal OX y las rectas verticales de ecuaciones x = a y x = b.
La integral definida de la función entre los extremos del intervalo [a, b] se denota como:

Propiedades de la integral definida

La integral definida cumple las siguientes propiedades:

Toda integral extendida a un intervalo de un solo punto, [a, a], es igual a cero.
Cuando la función f (x) es mayor que cero, su integral es positiva; si la función es menor que cero, su integral es negativa.
La integral de una suma de funciones es igual a la suma de sus integrales tomadas por separado.
La integral del producto de una constante por una función es igual a la constante por la integral de la función (es decir, se puede «sacar» la constante de la integral).
Al permutar los límites de una integral, ésta cambia de signo.
Dados tres puntos tales que a < b < c, entonces se cumple que (integración a trozos):
Para todo punto x del intervalo [a,b] al que se aplican dos funciones f (x) y g (x) tales que f (x) £ g (x), se verifica que:

Ilustración gráfica del concepto de integral definida.

Función integral

Considerando una función f continua en [a, b] y un valor x Î [a, b], es posible definir una función matemática de la forma:

donde, para no inducir a confusión, se ha modificado la notación de la variable independiente de x a t. Esta función, simbolizada habitualmente por F (x), recibe el nombre de función integral o, también, función área pues cuando f es mayor o igual que cero en [a, b], F (x) nos da el área.

Interpretación geométrica de la función integral o función área.

Teorema fundamental del cálculo integral

La relación entre derivada e integral definida queda establecida definitivamente por medio del denominado teorema fundamental del cálculo integral, que establece que, dada una función f (x), su función integral asociada F (x) cumple necesariamente que:

A partir del teorema fundamental del cálculo integral es posible definir un método para calcular la integral definida de una función f (x) en un intervalo [a, b], denominado regla de Barrow:

Se busca primero una función F (x) que verifique que F¿ (x) = f (x).
Se calcula el valor de esta función en los extremos del intervalo: F (a) y F (b).
El valor de la integral definida entre estos dos puntos vendrá entonces dado por:

Integral indefinida

Integral indefinida es el conjunto de las infinitas primitivas que puede tener una función.

Se representa por ∫ f(x) dx.

Se lee : integral de x diferencial de x.

∫ es el signo de integración.

f(x) es el integrando o función a integrar.

dx es diferencial de x, e indica cuál es la variable de la función que se integra.

C es la constante de integración y puede tomar cualquier valor numérico real.

Si F(x) es una primitiva de f(x) se tiene que:

∫ f(x) dx = F(x) + C

Para comprobar que la primitiva de una función es correcta basta con derivar.

Propiedades de la integral indefinida

1. La integral de una suma de funciones es igual a la suma de las integrales de esas funciones.

∫[f(x) + g(x)] dx =∫ f(x) dx +∫ g(x) dx

2. La integral del producto de una constante por una función es igual a la constante por la integral de la función.

∫ k f(x) dx = k ∫f(x) dx

domingo, 3 de marzo de 2013

Ejemplo
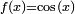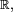Una primitiva de la función $\scriptstyle f(x)=\cos(x)$ en $\scriptstyle \mathbb{R},$ es la función $\scriptstyle F(x)=\sin(x)$ ya que:

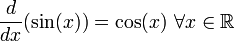
$\frac{d}{dx}(\sin(x))=\cos(x)\ \forall x\in\mathbb{R}$

Dado que la derivada de una constante es cero, tendremos que cos(x) tendrá un número infinito de primitivas tales como sin(x), sin(x) + 5, sen(x) - 100, etc. Es más, cualquier primitiva de la función f(x) = cos(x) será de la forma sin(x) + C donde C es una constante conocida como constante de integración.

Aquí están las principales funciones primitivas:

Función $F \,\!$ : primitiva de $f \,\!$	función $f \,\!$ : derivada de $F \,\!$
$f\left(x\right) = \frac {x^{n+1}}{n+1} + k \,\!$	$\begin{matrix}f'\left(x\right) = x^n & & \mathrm{ , para} & n \neq -1 \end{matrix} \,\!$
$f\left(x\right) = e^x + k \,\!$	$f'\left(x\right) = e^x \,\!$
$f\left(x\right) = \ln\left(x\right) + k \,\!$	$f'\left(x\right) = \frac{1}{x} \,\!$
$f\left(x\right) = \frac {x^{1-n}}{1-n} + k \,\!$	$\begin{matrix}f'\left(x\right) = \frac {1}{x^n} & & \mathrm{ , para} & n \neq 1 \end{matrix} \,\!$
$f\left(x\right) = -\cos\left(x\right) + k \,\!$	$f'\left(x\right) = \sin\left(x\right) \,\!$
$f\left(x\right) = \sin\left(x\right) + k \,\!$	$f'\left(x\right) = \cos\left(x\right) \,\!$
$f\left(x\right) = \tan\left(x\right) + k \,\!$	$f'\left(x\right) = \frac {1}{\cos^2\left (x\right)} \,\!$
$\begin{matrix}f\left(x\right) = \frac {a^x}{\ln(a)} + k & & \mathrm{, si} & a > 0 \end{matrix} \,\!$	$f'\left(x\right) = a^x \,\!$
$f\left(x\right) = \frac {2}{3} \sqrt{x}^3 + k \,\!$	$f'\left(x\right) = \sqrt {x} \,\!$
$f\left(x\right) = ax + k \,\!$	$f'\left(x\right) = a \,\!$
$f\left(x\right) = \arctan(x) + k \,\!$	$f'\left(x\right) = \frac{1}{1+x^2} \,\!$

Volumen

Datos para hallar el área y volumen de la esfera respecto del cilindro circunscrito.

El volumen de una esfera es 2/3 del volumen del cilindro circunscrito a la esfera. Su base es un círculo del mismo diámetro que la esfera. Su altura tiene la misma medida que dicho diámetro:

$V = \frac{2}{3} (\pi r^2 \cdot 2r)$

$V = \frac{4\pi r^3}{3}$

donde V es el volumen de la esfera y r el radio.
Esta relación de volúmenes se adjudica a Arquímedes.

Es posible calcular el volumen de una esfera con un margen de error aproximado al 0.03% sin utilizar el valor de π:

$V = \frac{67}{16} r^3$

Área

El área es 4 veces pi por su radio al cuadrado.

$\ A = 4\pi r^2$

Demostración
Arquímedes demostró que el área de la esfera es dos tercios respecto al del cilindro usando esta definición: $A = \frac{2}{3} (2r \cdot 2\pi r + 2 \cdot \pi r^2)$ $A = \frac{2}{3} (4\pi r^2 + 2\pi r^2)$ $A = \frac{2}{3} (6\pi r^2)$ $A = 4\pi r^2$

Demostración
El área de la esfera es también igual a la derivada de su volumen con respecto a r. $V = \frac{4}{3}\pi r^3 = \int_{0}^{r}A(r) dr$ $\frac{dV}{dr}= A(r) = 4\pi r^2$

matematicas