matematicas

Volumen

Datos para hallar el área y volumen de la esfera respecto del cilindro circunscrito.

El volumen de una esfera es 2/3 del volumen del cilindro circunscrito a la esfera. Su base es un círculo del mismo diámetro que la esfera. Su altura tiene la misma medida que dicho diámetro:

$V = \frac{2}{3} (\pi r^2 \cdot 2r)$

$V = \frac{4\pi r^3}{3}$

donde V es el volumen de la esfera y r el radio.
Esta relación de volúmenes se adjudica a Arquímedes.

Es posible calcular el volumen de una esfera con un margen de error aproximado al 0.03% sin utilizar el valor de π:

$V = \frac{67}{16} r^3$

Área

El área es 4 veces pi por su radio al cuadrado.

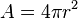
$\ A = 4\pi r^2$

Demostración
Arquímedes demostró que el área de la esfera es dos tercios respecto al del cilindro usando esta definición: $A = \frac{2}{3} (2r \cdot 2\pi r + 2 \cdot \pi r^2)$ $A = \frac{2}{3} (4\pi r^2 + 2\pi r^2)$ $A = \frac{2}{3} (6\pi r^2)$ $A = 4\pi r^2$

Demostración
El área de la esfera es también igual a la derivada de su volumen con respecto a r. $V = \frac{4}{3}\pi r^3 = \int_{0}^{r}A(r) dr$ $\frac{dV}{dr}= A(r) = 4\pi r^2$

matematicas

domingo, 3 de marzo de 2013

Área

No hay comentarios:

Publicar un comentario

Seguidores

Archivo del blog

Datos personales