Por ejemplo, puede probarse que la siguiente ecuación define una función implícita en cierta región de
 entre las variables x e y:
entre las variables x e y:Diferenciación
Para poder derivar una función implícita se usa la regla de la cadena, en el caso de la variable independiente no hay problema ya que se deriva directamente, para la variable dependiente se considera como una función que a su vez está en función de la variable independiente:Dada una función
 , implícita, si queremos calcular la derivada de y respecto de x:
, implícita, si queremos calcular la derivada de y respecto de x:  .
.Si consideramos
 es una función en términos de la variable independiente x y
es una función en términos de la variable independiente x y  es una función en términos de la variable dependiente y, dado que
es una función en términos de la variable dependiente y, dado que  , entonces para obtener la derivada:
, entonces para obtener la derivada:Ejemplo
Obtener la derivada de: se puede considerar que son dos funciones,
se puede considerar que son dos funciones,  y
y  por lo que se derivará como un producto:
por lo que se derivará como un producto: se deriva como:
se deriva como: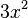 se deriva de forma normal como:
se deriva de forma normal como: se puede considerar como un producto y se deriva como:
se puede considerar como un producto y se deriva como: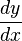 ) los valores son:
) los valores son: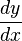 se obtiene la derivada de la función implícita:
se obtiene la derivada de la función implícita:


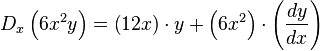




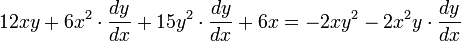
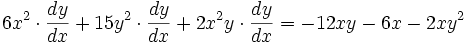



 , se puede escribir
, se puede escribir




 , se puede escribir como
, se puede escribir como
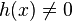 , entonces la regla dice que la derivada de
, entonces la regla dice que la derivada de  es igual a:
es igual a:![\frac{d}{dx}f(x) = f'(x) = \frac{g'(x)h(x) - g(x)h'(x)}{[h(x)]^2}](http://upload.wikimedia.org/math/b/b/3/bb36df8c011f8e7202d7ae273feca2cd.png)





![f'(x) = \frac{\cos(x)\cos(x) - \sin(x)[-\sin(x)]}{\cos^2(x)}](http://upload.wikimedia.org/math/d/f/6/df62b96bb8d3a2fb6df1394b9116d435.png)

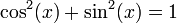
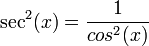
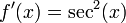


 , se puede escribir
, se puede escribir




