Si f(x) = cos(x)
 , se puede escribir
, se puede escribirDerivada de la función tangente
A partir de la regla del cociente, según la cual si la función que se quiere derivar, , se puede escribir como
, se puede escribir como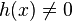 , entonces la regla dice que la derivada de
, entonces la regla dice que la derivada de  es igual a:
es igual a:
 , se puede escribir
, se puede escribir




 , se puede escribir como
, se puede escribir como
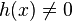 , entonces la regla dice que la derivada de
, entonces la regla dice que la derivada de  es igual a:
es igual a:![\frac{d}{dx}f(x) = f'(x) = \frac{g'(x)h(x) - g(x)h'(x)}{[h(x)]^2}](http://upload.wikimedia.org/math/b/b/3/bb36df8c011f8e7202d7ae273feca2cd.png)





![f'(x) = \frac{\cos(x)\cos(x) - \sin(x)[-\sin(x)]}{\cos^2(x)}](http://upload.wikimedia.org/math/d/f/6/df62b96bb8d3a2fb6df1394b9116d435.png)

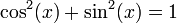
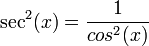
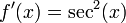
No hay comentarios:
Publicar un comentario