El
cálculo diferencial es una parte importante del análisis matemático y dentro del mismo del
cálculo. Consiste en el estudio del cambio de las variables dependientes cuando cambian las variables independientes de las funciones o campos objetos del análisis. El principal objeto de estudio en el cálculo diferencial es
la derivada. Una noción estrechamente relacionada es la de
diferencial de una función.
En el estudio del cambio de una función, es decir, cuando cambian sus variables independientes es de especial interés para el cálculo diferencial el caso en el que el cambio de las variables es infinitesimal, esto es, cuando dicho cambio tiende a cero (se hace tan pequeño como se desee). Y es que el cálculo diferencial se apoya constantemente en el concepto básico del
límite. El paso al límite es la principal herramienta que permite desarrollar la teoría del cálculo diferencial y la que lo diferencia claramente del álgebra.
Desde el punto de vista matemático de las
funciones y la geometría, la derivada de una función en un cierto
punto es una medida de la tasa en la cual una función
cambia conforme un
argumento se modifica. Esto es, una derivada involucra, en términos matemáticos, una
tasa de cambio. Una derivada es el cálculo de las pendientes instantáneas de

en cada punto

. Esto se corresponde a las
pendientes de las
tangentes de la
gráfica de dicha función en sus puntos (una tangente por punto); Las derivadas pueden ser utilizadas para conocer la
concavidad de una función, sus intervalos de crecimiento, sus máximos y mínimos.
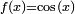 en
en 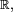 es la función
es la función  ya que:
ya que: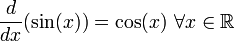
 : primitiva de
: primitiva de 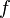
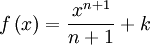

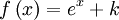
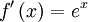
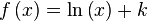

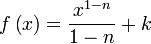

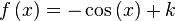

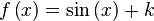

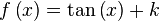

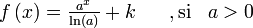
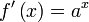
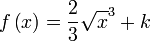

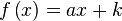

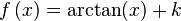









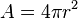



 en cada punto
en cada punto  . Esto se corresponde a las
. Esto se corresponde a las